Beyond Pretty Pictures: Trusting Your Results with CFD Verification and Validation (Part 1)

Eye-catching visualizations are just the tip of the iceberg in CFD. As researchers, we need to go beyond “Colorful Fluid Dynamics” and ensure the reliability of our simulations. This guide dives into Verification and Validation (VV) – the cornerstone of building trust in your CFD results. We’ll explore the key concepts of VV and equip you to confidently answer the crucial question: “How can I trust this?”

“Colorful Fluid Dynamics” - an ingenious play on words within the realm of Computational Fluid Dynamics (CFD). This clever pun, coined by Dr. Phil Roe during his lecture series, “Colorful Fluid Dynamics: Behind the Scenes,” not only adds a touch of humor to the technical field but also underscores a fundamental truth about the power and potential pitfalls of CFD. Dr. Roe’s assertion that “Even inaccurate CFD can be useful” might initially raise eyebrows, but it touches upon a deeper reality: the ability of detailed visualization to enrich CFD with information surpassing that of traditional experiments. However, as Dr. Doug McLean a Boeing Technical Fellow, aptly notes “These days it is common to see a complicated flow field, predicted with all the right general features and displayed in glorious detail that looks like the real thing. Results viewed in this way take on an air of authority out of proportion to their accuracy. In this regard, modern CFD is a very seductive thing”. Indeed, while modern CFD simulations may appear incredibly lifelike, their authority can be misleading if not backed by rigorous verification and validation processes.

In the words of Queen’s timeless query in Bohemian Rhapsody, “Is this the real life? Is this just fantasy?” - a sentiment that resonates deeply within the realm of CFD. How can we be certain that our numerical models faithfully represent physical reality? How do we ensure that our results remain robust across different mesh resolutions? These questions form the cornerstone of any meaningful discussion surrounding CFD results.

For researchers delving into the intricate world of CFD, the journey begins with a commitment to thorough verification and validation. These twin pillars, standing tall before any discussion of results, serve as the litmus test for the trustworthiness of findings. Through meticulous examination of code errors and simulation results, verification and validation offer the assurance needed to confidently interpret and defend CFD outcomes. Indeed, flip through the pages of any research paper utilizing CFD, and you’re bound to encounter a dedicated section addressing the verifications and validations undertaken. In the forthcoming discussion, we’ll delve into the essence of verification and validation, unveiling essential tips and strategies to fortify your CFD endeavors.

So, without further ado, let’s embark on this journey of discovery and enlightenment within the dynamic realm of Colorful Fluid Dynamics.

Base Case

In this guide, we’ll navigate the intricacies of verification and validation in Computational Fluid Dynamics (CFD) through the lens of a fundamental problem: the steady-state one-dimensional convection-diffusion equation. This equation, with fixed (Dirichlet) boundary conditions at both ends, serves as an ideal platform for illustrating key concepts in CFD verification and validation.

Let’s start with the equation itself:

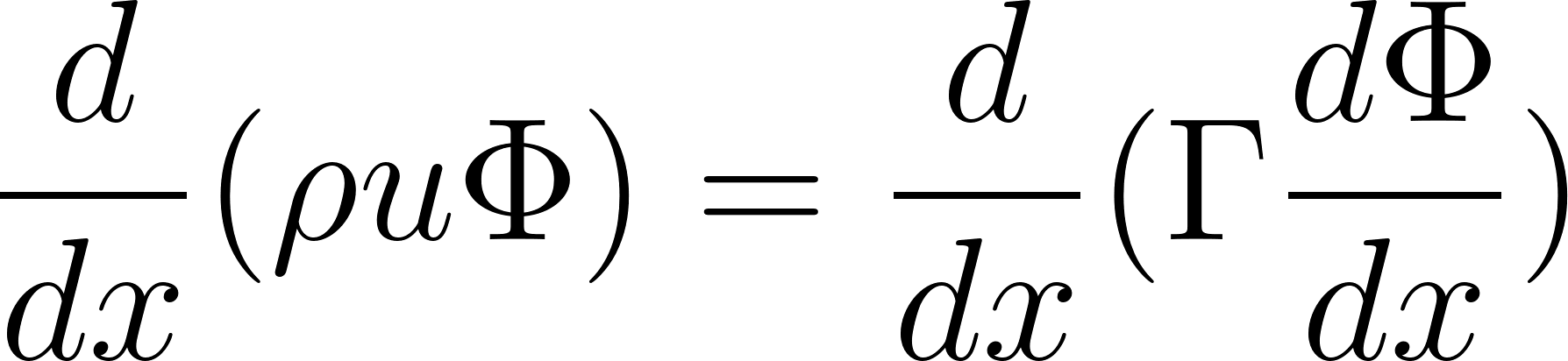
Accompanied by boundary conditions: Phi = Phi(0) at x = 0, and Phi = Phi(L) at x = L. Here, we assume constant density and velocity. Although seemingly straightforward, this equation encapsulates the delicate interplay between convection and diffusion in a one-dimensional domain. The analytical solution to this problem is as follows:

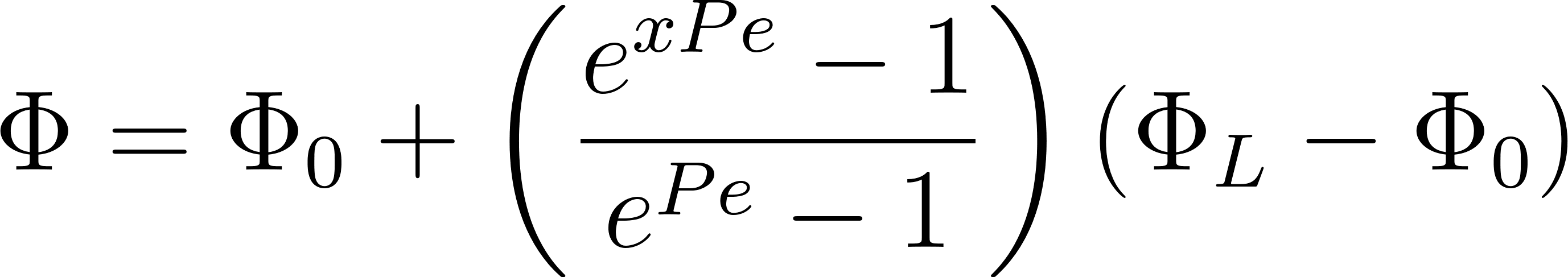
where the Peclet number, a critical parameter in convection-diffusion problems, is defined as:

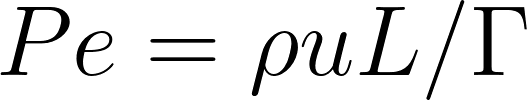
This particular problem holds immense significance as a benchmark for testing numerical methods, encompassing both discretization and solution schemes. While its simplicity belies its importance, it serves as a litmus test for the accuracy and robustness of numerical techniques in handling convection-diffusion phenomena. Physically, this problem represents a scenario where convection is precisely balanced by diffusion along the streamwise direction. While such equilibrium is rare in practical flows, this idealized case offers invaluable insights into the behavior of numerical methods.

For the purpose of this article, employing a problem with an exact solution is paramount to underscore the principles of verification and validation in CFD. It provides a tangible reference point for evaluating the accuracy of numerical simulations and validating their predictive capabilities against analytical solutions.

To facilitate understanding and implementation, an easy-to-follow Python code is provided here for the readers to test out.

Verification

Verification assessment in Computational Fluid Dynamics (CFD) serves as a crucial step in ensuring the accuracy and reliability of numerical simulations. At its core, verification evaluates the fidelity of the computational implementation of the conceptual model against exact analytical solutions. In essence, it seeks to verify that the programming faithfully represents the developer’s intended model and solution.

In the realm of CFD, verification extends beyond mere code correctness to encompass a deeper understanding of the variables that can significantly influence simulation outcomes. One such variable that warrants careful scrutiny is the mesh. The mesh, or numerical grid, serves as the foundation of discretizing the computational domain, dividing it into discrete points for solving governing equations. Mesh quality plays a pivotal role in determining the accuracy of CFD simulations. To ensure robustness, it’s imperative to obtain results that remain unaffected by changes in mesh size or shape. A comprehensive mesh sensitivity analysis becomes paramount in this regard, offering insights into the mesh’s influence on simulation outcomes.

Conducting a mesh sensitivity analysis involves repeating simulations using different mesh configurations until convergence is achieved. This iterative process allows for the identification of optimal mesh parameters that yield consistent and reliable results independent of mesh variations. Ultimately, achieving mesh-independent results instills confidence in the accuracy of CFD simulations, validating their alignment with the underlying conceptual model. However, it’s important to note that while mesh sensitivity analysis enhances confidence in simulation accuracy, it primarily addresses issues related to mesh quality rather than inherent flaws in the model itself. To comprehensively assess the model’s robustness, additional validation steps, such as comparison with experimental data or theoretical predictions, may be necessary.

In summary, verification in CFD involves meticulous scrutiny of numerical implementations to ensure alignment with the intended conceptual model. By conducting thorough mesh sensitivity analyses, CFD practitioners can ascertain the accuracy and reliability of simulations, laying a solid foundation for further validation and application of computational models in real-world scenarios.

Let’s delve into the intricacies of grid sensitivity or mesh independence analysis through the lens of the 1D Convection-Diffusion equation solved using the Finite Volume Method (FVM). In this illustrative example, we’ll explore a one-dimensional domain spanning 1 meter, with boundary conditions of 1 and 2 at either end. Using a velocity of 10 m/s resulting in a Peclet number of 50, alongside constants such as density 1 and a Gamma value of 0.2, we attempt to understand how variations in grid resolution affect numerical solutions.

The computational domain is discretized, or meshed, to facilitate numerical computation via the Finite Volume Method, employing a central-difference scheme with second-order accuracy. Maintaining consistency across simulations, we systematically increase the number of grid points, starting from a coarse grid with 16 cells. With each subsequent run, we halve the grid size, effectively doubling the number of grid points. We analyze the results obtained for grid resolutions of 16, 32, 64, 128, 256, and 512 grid points, alongside the analytical solution.

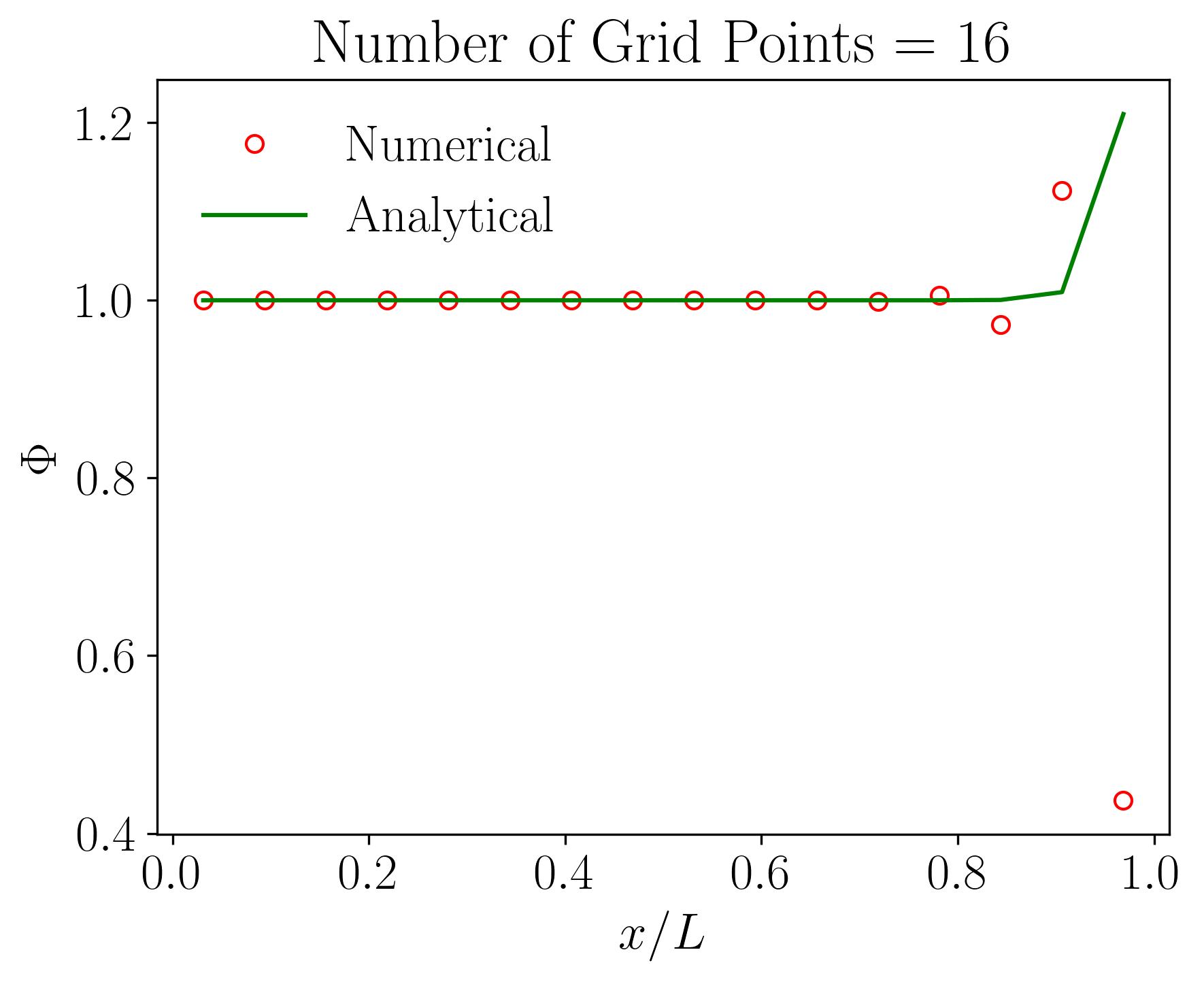
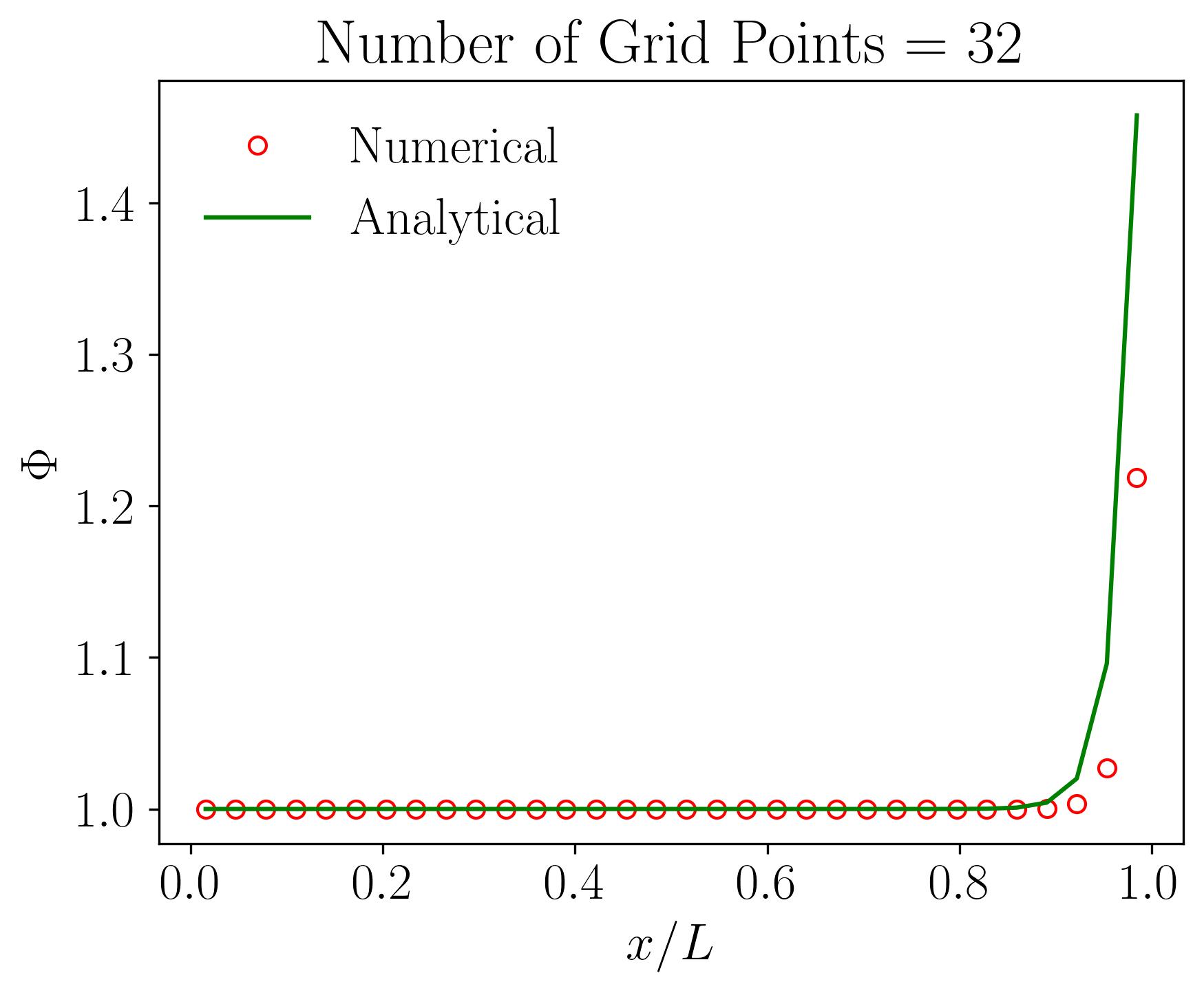
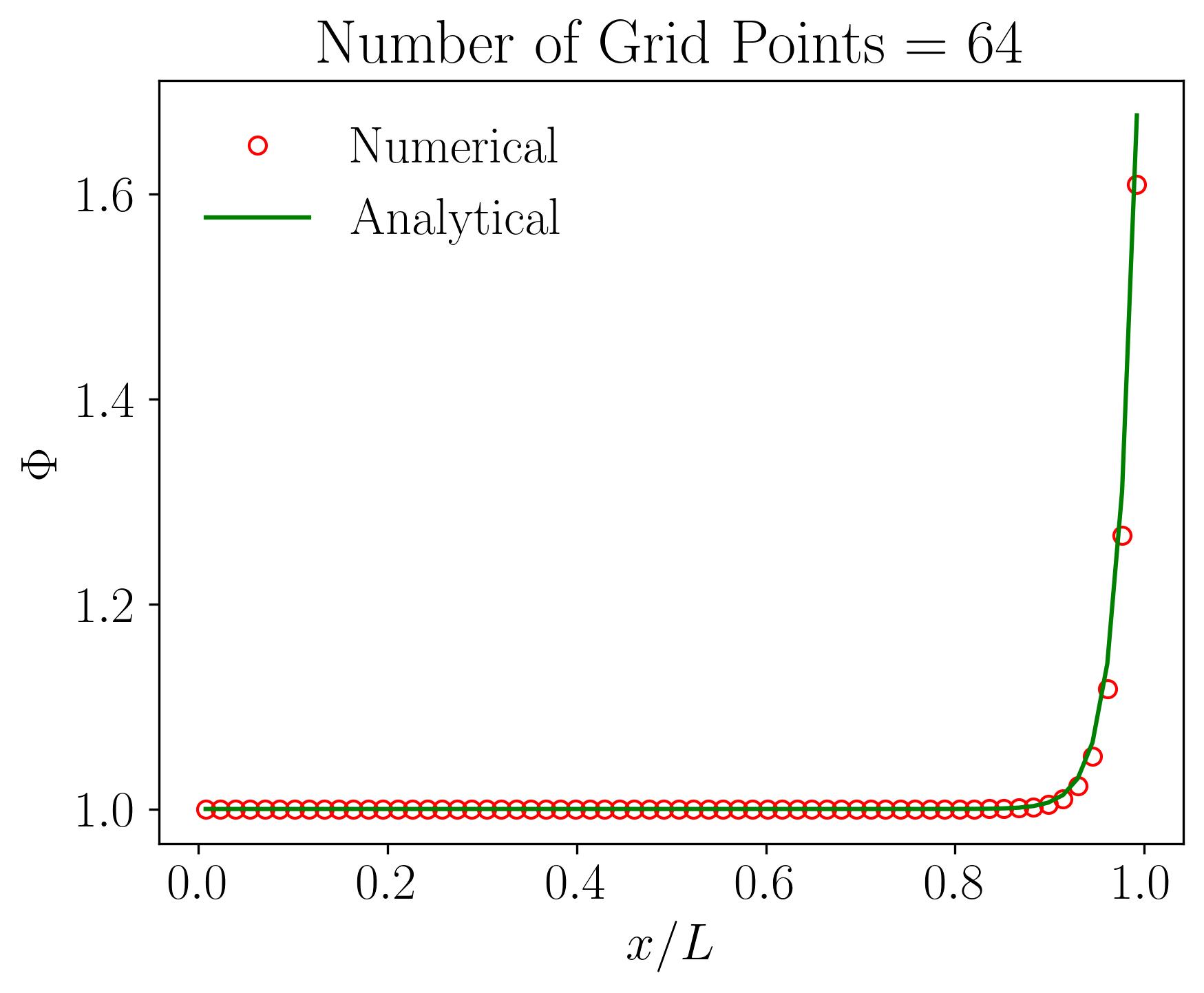
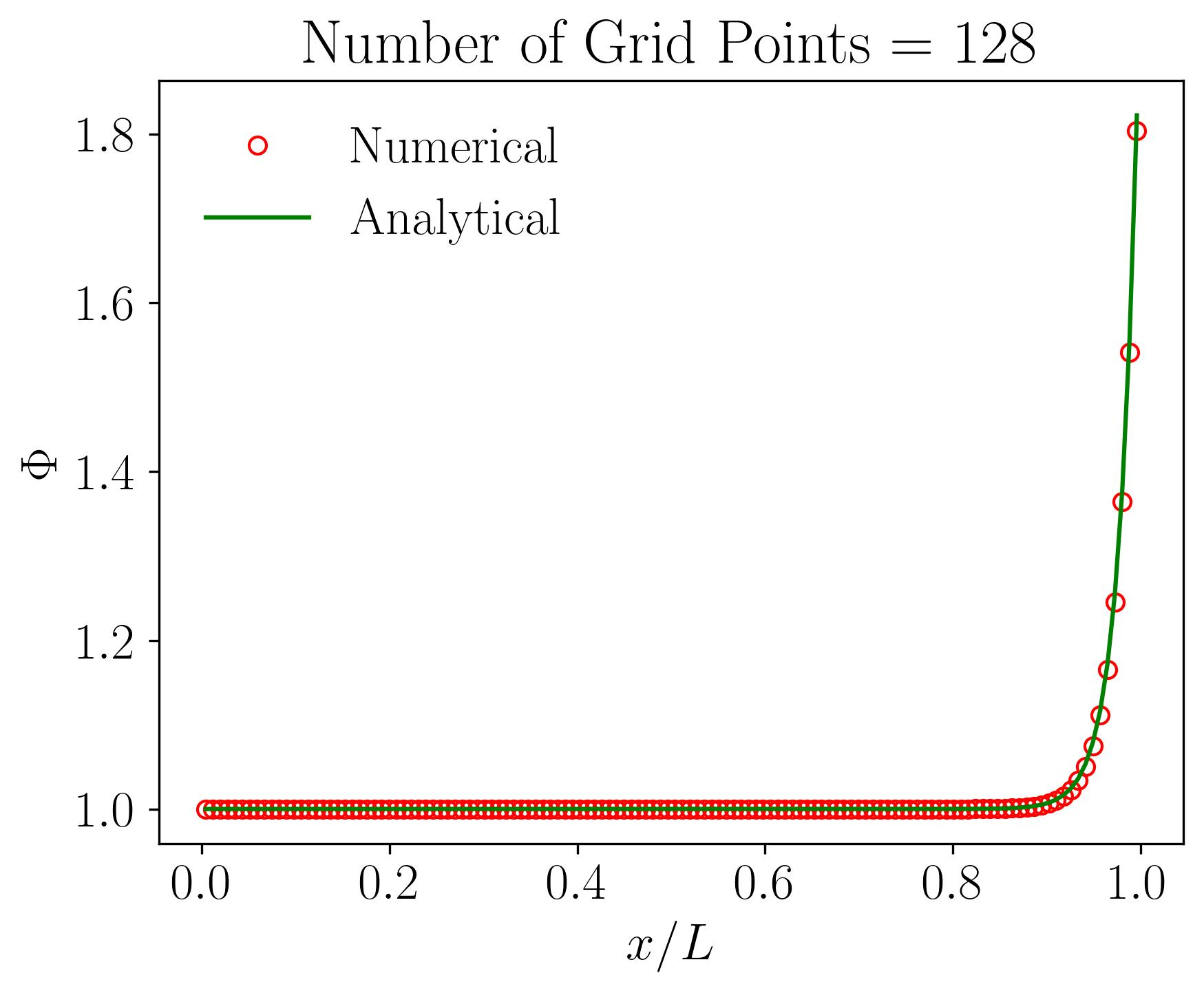
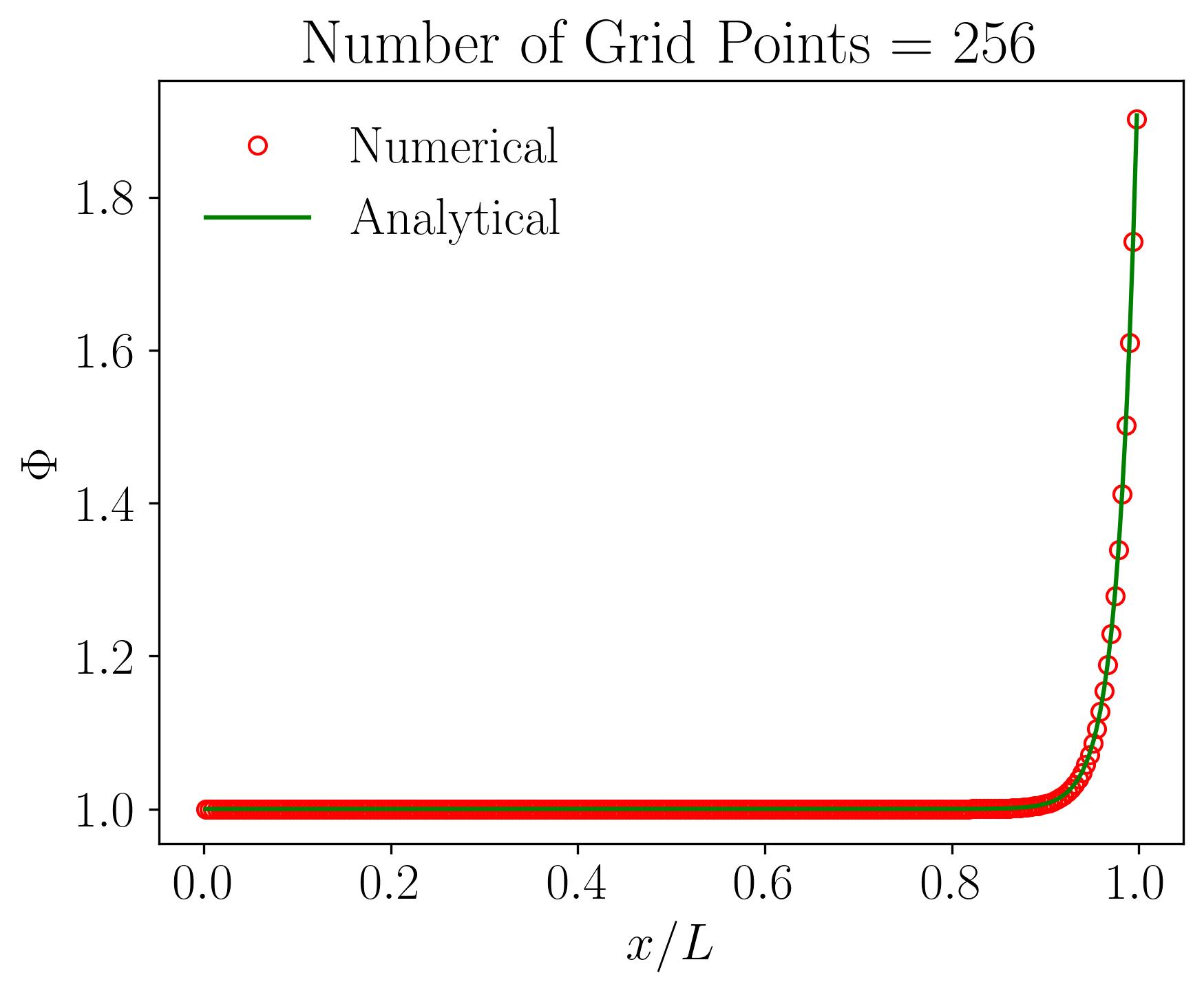
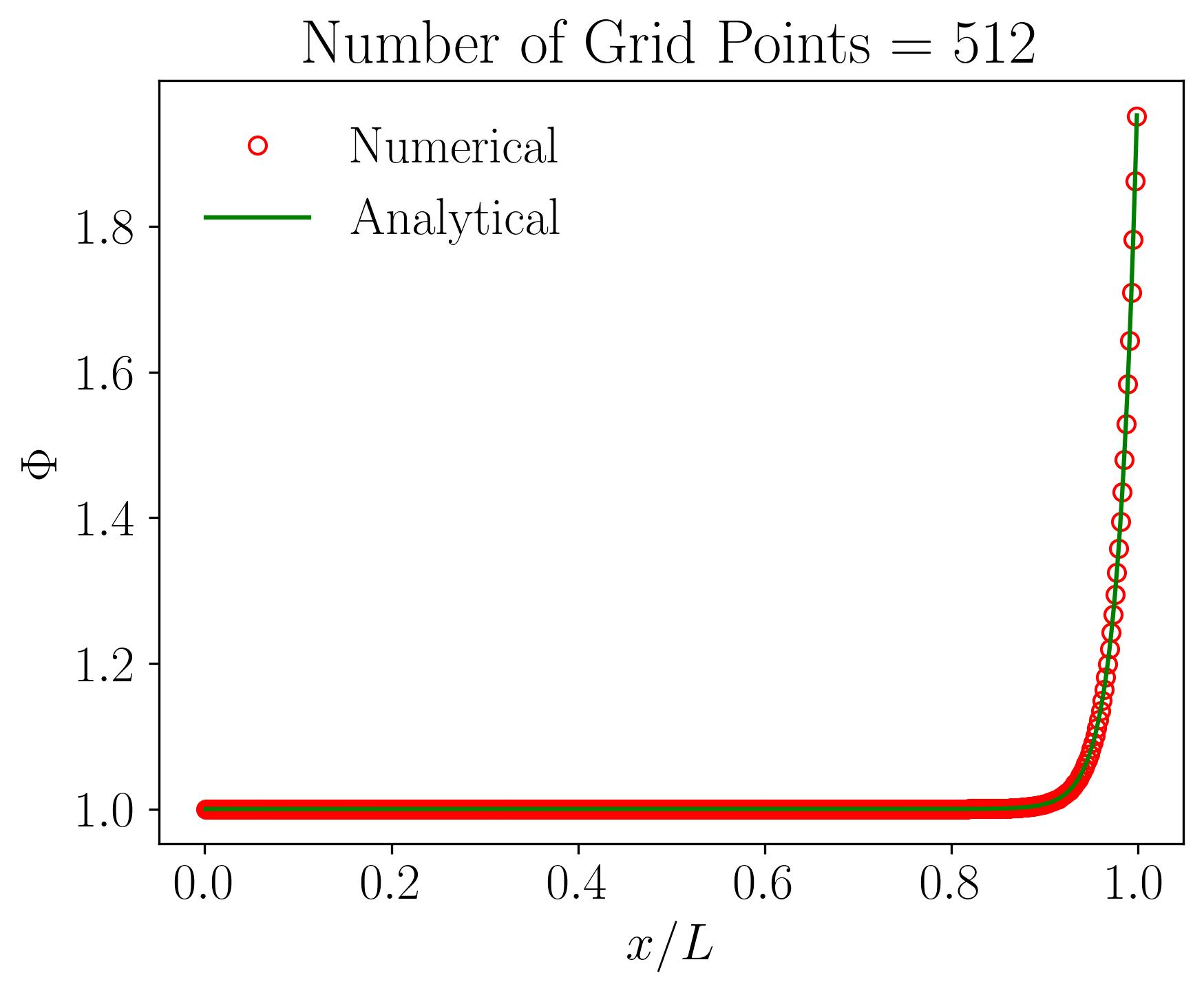
Initially, employing a coarse grid with only 16 points reveals a notable deviation between numerical and analytical solutions. However, as we progressively increase the number of grid points, the disparity diminishes. Eventually, with 512 grid points, the numerical and analytical solutions converge, demonstrating grid or mesh independence. In simpler terms, further increases in grid resolution do not significantly alter the numerical solution compared to the analytical counterpart. This critical analysis, known as grid sensitivity or mesh independence analysis, is fundamental in validating the robustness of numerical simulations.

Taking our analysis a step further, we focus on tracking the value of Phi at a specific point within our domain, preferably closer to the exit boundary (x = L). This region, termed the critical region or region of interest, experiences significant gradient changes, making it ideal for assessing numerical convergence across multiple mesh resolutions.

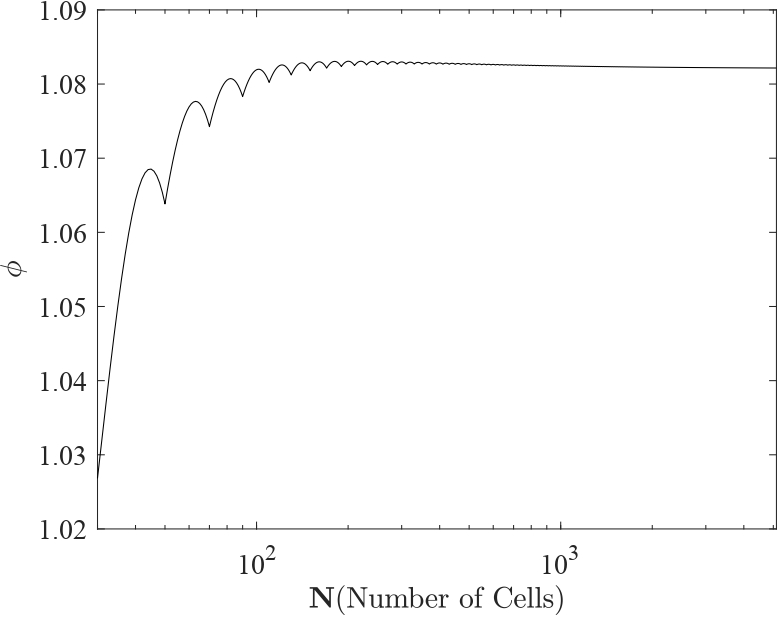
By monitoring Phi across various mesh resolutions, we observe a convergence towards a consistent value as the number of grid points increases. Initially, with fewer than 1000 grid points, oscillations may be observed in the results. However, with a further increase in grid resolution, these oscillations dampen, and the solution stabilizes within an asymptotic region, demonstrating convergence. This phenomenon lies at the heart of verification in CFD. While grid sensitivity analysis is a cornerstone of verification in CFD, it’s worth noting that other methodologies exist, which we’ll explore in subsequent discussions. However, no study in CFD is complete without addressing mesh independence, as it forms the bedrock of confidence in numerical results.

Validation

Upon completion of the verification process, where the stability of simulation results is confirmed with grid refinement, the next crucial step is validation. While verification ensures the accuracy of the computational simulation relative to the conceptual model, validation assesses whether the simulation aligns with physical reality. It scrutinizes the physics embedded within the implemented computational model, typically CFD, by comparing simulation results with experimental data.

Let’s understand this using the example of one-dimensional convection-diffusion equation. This equation’s unique attribute, unlike many other CFD models, is its possession of an analytical solution. Following the mesh independence analysis, which determined that 512 grid points were adequate for this problem, the relative error between numerical and analytical results is found to be negligible. Thus, the numerical model for the one-dimensional convection-diffusion equation can be deemed validated. This epitomizes the essence of validation – comparing the numerical model to an analytical or experimental benchmark.

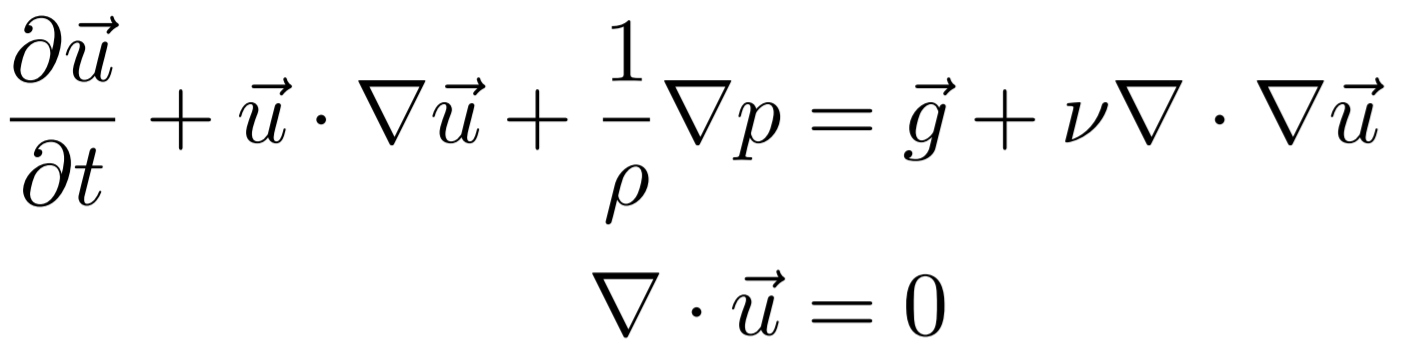
However, consider for a moment: is it always feasible to obtain analytical or experimental benchmarks for every problem? Regrettably, the answer is no. The Navier-Stokes equations, for instance, are predominantly nonlinear due to their convective terms, rendering analytical solutions elusive. In fact, the existence and smoothness of solutions for Navier-Stokes equations in three dimensions constitute one of the seven Clay “Millennium Problems,” offering a hefty $1 million prize for resolution.

Consequently, reliance on experimental data becomes pivotal. While experimental validation is practical and accessible for many scenarios, it remains challenging for certain specialized problems. Nevertheless, innovative approaches can circumvent these limitations. For instance, in the absence of experimental data for a specific problem configuration, researchers can validate their numerical setup against available experiments with similar parameters. For example, if investigating the flow past a circular cylinder at a Reynolds number of 2500 using OpenFOAM, researchers may struggle to find corresponding experimental data. In such cases, running simulations at a different Reynolds number, where experimental data is available, enables comparative validation of the numerical setup.

This approach has gained traction in recent literature, where researchers often encounter challenges associated with the absence of experimental benchmarks tailored to their specific simulation parameters. While validation in CFD may pose inherent difficulties, innovative strategies empower researchers to bridge the gap between numerical simulations and physical reality, advancing our understanding and application of computational models in diverse fields.

In summary, the journey through verification and validation in Computational Fluid Dynamics (CFD) illuminates the intricate process of ensuring the accuracy and reliability of numerical simulations. Through verification, we ascertain the fidelity of our computational implementations to the intended conceptual models, while validation bridges the gap between simulation outcomes and physical reality by comparing them with analytical or experimental benchmarks. The exploration of verification unveils the importance of grid sensitivity analysis, where the convergence of numerical solutions with increasing grid resolution signifies robustness and accuracy. Meanwhile, validation underscores the challenge of aligning numerical simulations with experimental data, particularly in complex systems like the Navier-Stokes equations, where analytical solutions remain elusive.

Ultimately, the synergy between verification and validation forms the cornerstone of rigorous and trustworthy CFD research. As we navigate the complexities of fluid dynamics and computational modeling, embracing these principles empowers us to unlock new insights, advance scientific understanding, and address real-world challenges with confidence.

Stay tuned for Part 2 of this blog series, where we’ll delve deeper into the realm of best practices for verification and validation, tailored specifically to CFD research. In the upcoming installment, we’ll uncover essential strategies, tools, and methodologies to elevate your CFD simulations to new heights of accuracy and reliability.

Happy Computing!!!