The world of science is brimming with complex systems, from weather patterns to neural networks. While mountains of data exist, extracting meaningful insights remains a challenge. Enter Dynamic Mode Decomposition (DMD), a powerful tool that unlocks the secrets hidden within this data. This article delves into DMD, exploring its capabilities and how it empowers researchers across diverse fields to achieve breakthroughs.

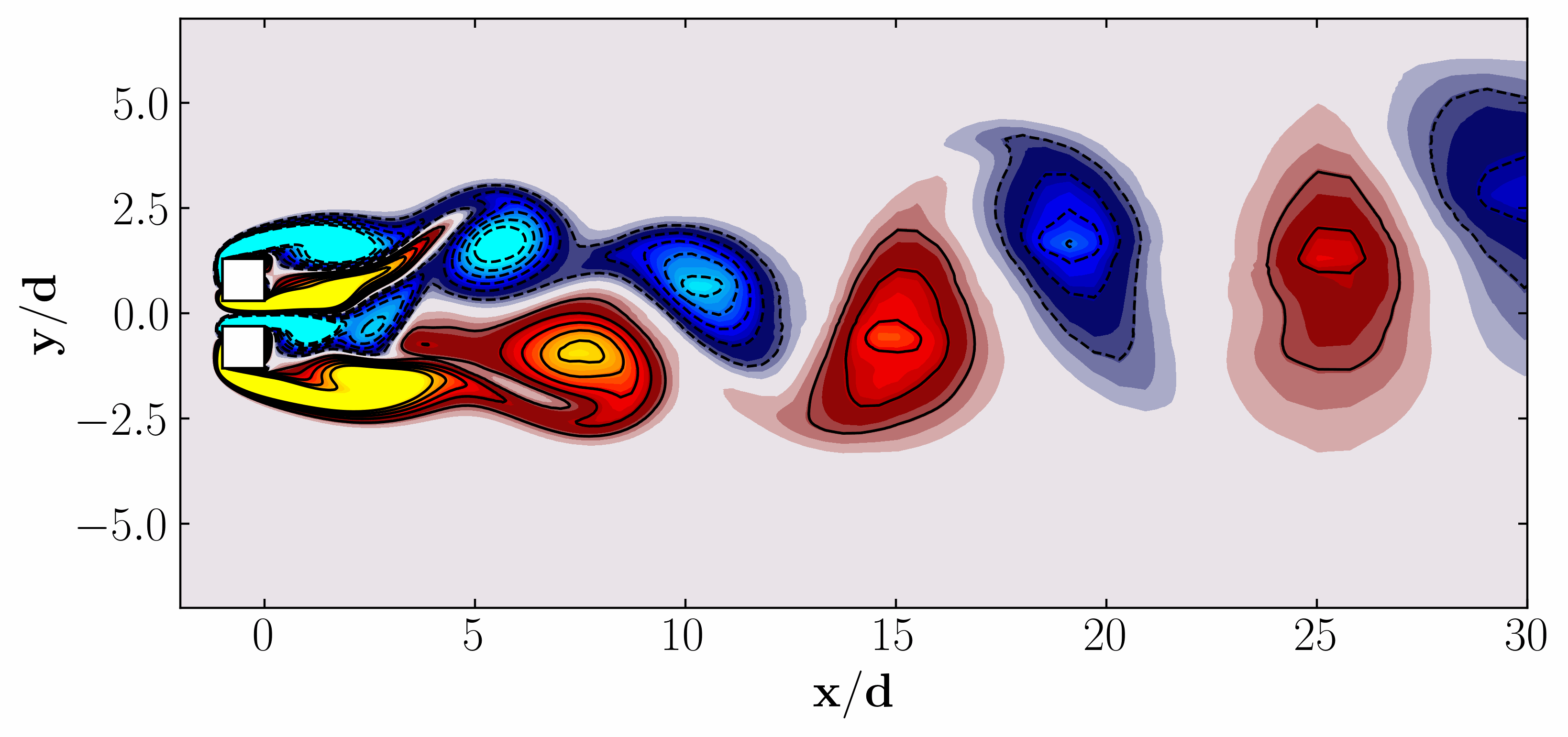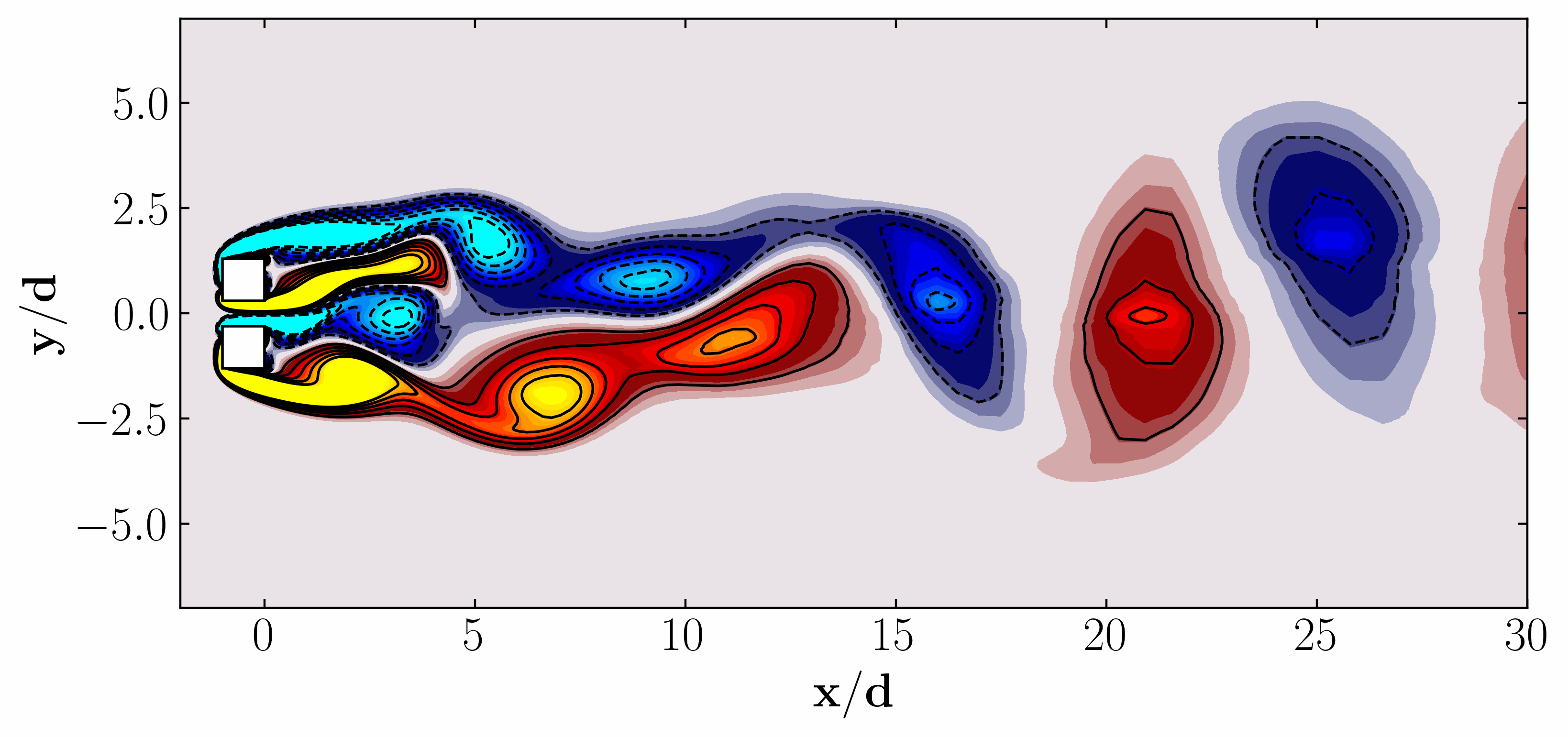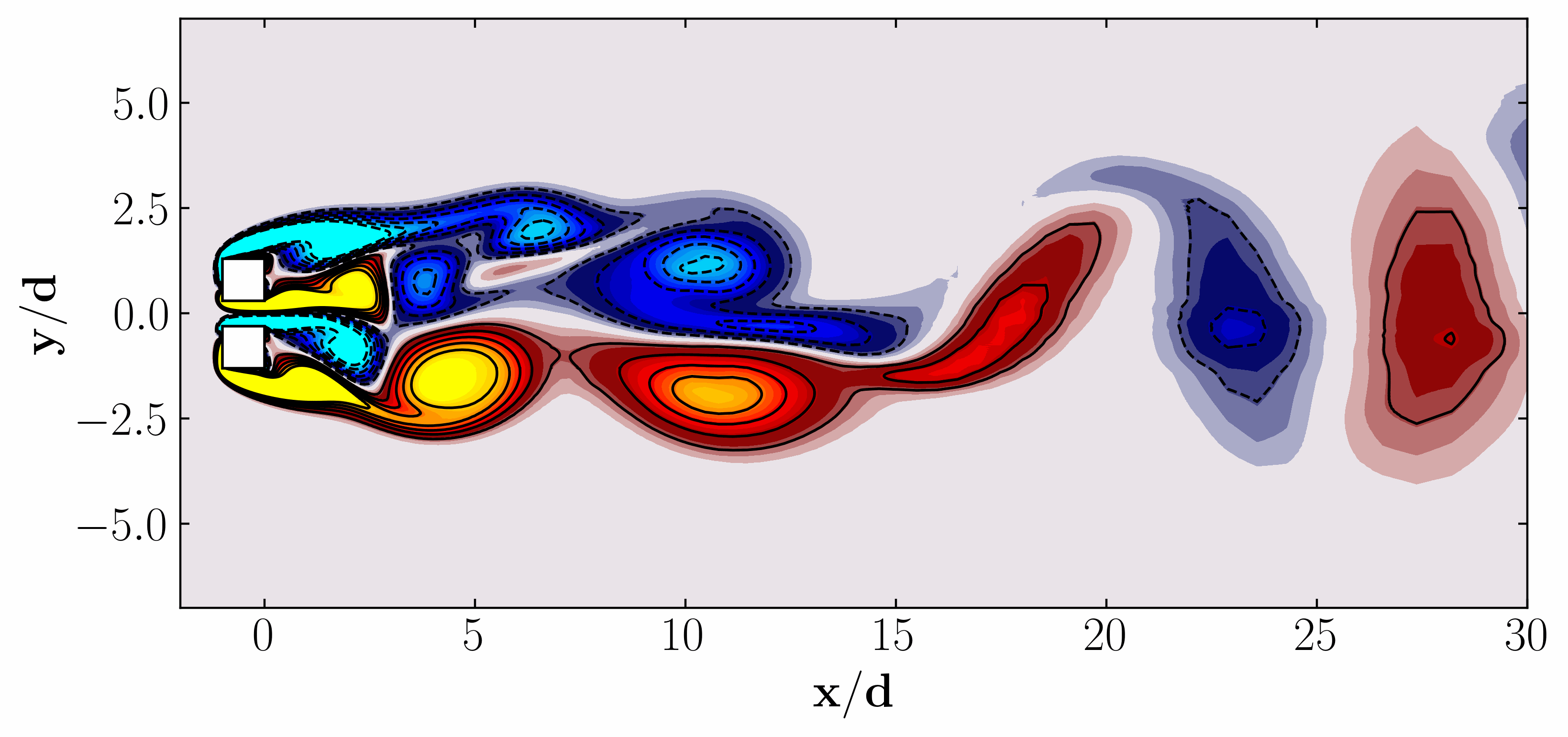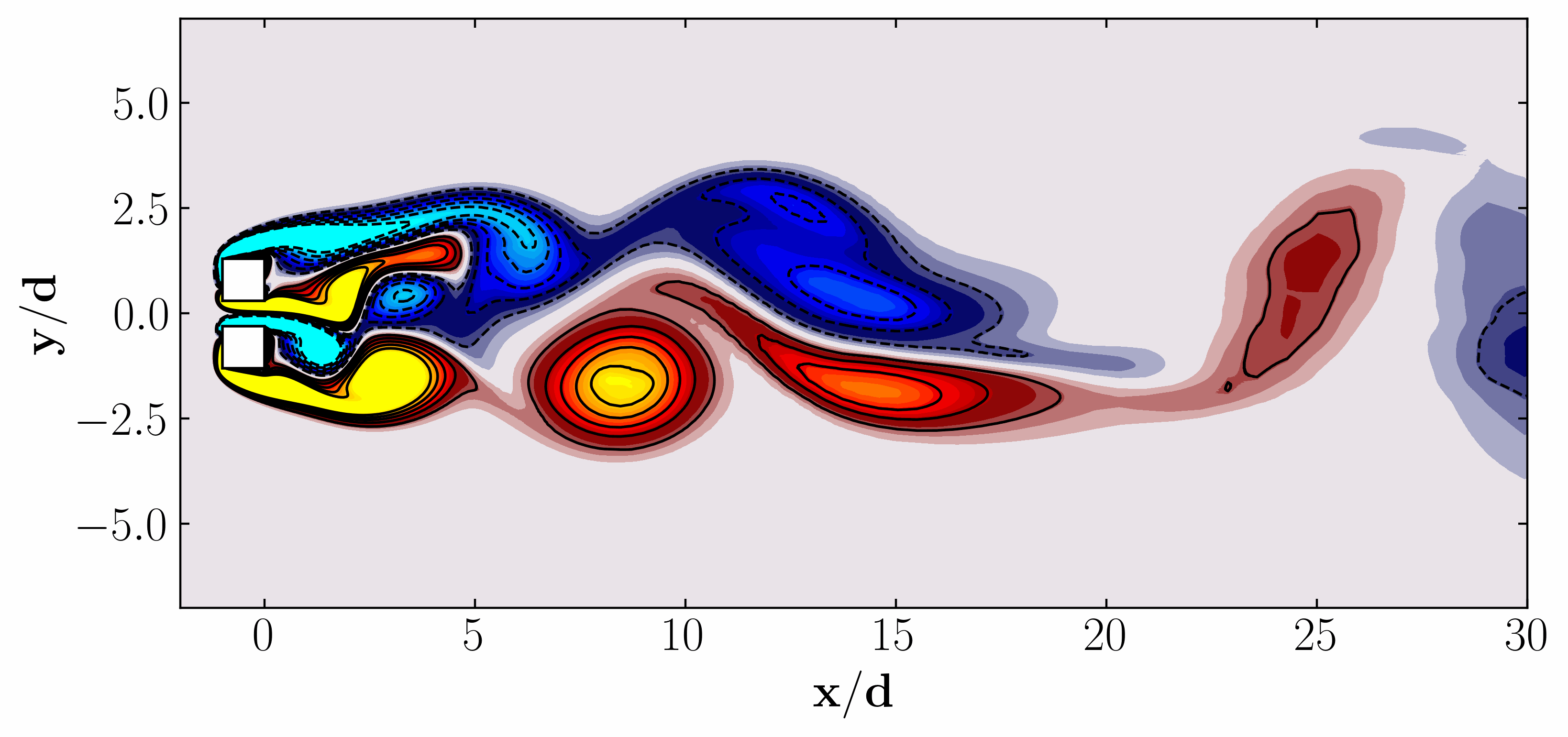
In the dynamic realm of data-driven modeling and control, the potential for transformative breakthroughs across engineering, biological, and physical sciences is immense. With an abundance of high-fidelity measurements sourced from historical records, numerical simulations, and experimental data, the landscape is ripe for innovation. Yet, amidst this wealth of data, the challenge lies in crafting elusive models that capture the complexity of modern systems. Imagine turbulent fluids, epidemiological networks, neural connections, financial markets, or the climate—each representing a high-dimensional, nonlinear dynamical systems, exhibiting intricate multiscale phenomena across space and time. Despite their complexity, these systems often reveal themselves through low-dimensional attractors, characterized by spatiotemporal coherent structures.

Enter Dynamic Mode Decomposition (DMD)—a potent tool at the forefront of discovery within dynamical systems. By leveraging DMD, researchers unlock the potential to extract these low-dimensional attractors, shedding light on the underlying dynamics hidden within the intricate systems of high-dimensional data.

In previous articles, my focus has been on Proper Orthogonal Decomposition (POD), a modal decomposition methodology designed to extract highly dominant, low-dimensional patterns from complex, dynamical systems like turbulent flows. Dynamic Mode Decomposition (DMD) stands as another modal reduction method, offering the capability to extract spatiotemporal coherent structures from your data. The increasing prominence of DMD can be attributed to its equation-free, data-driven nature, which allows for accurate decomposition of complex systems into spatiotemporal coherent structures. These structures, in turn, can be leveraged for short-term future-state prediction and control.

Continuing our exploration of modal reduction methods and data-driven systems, it’s time to dive into Dynamic Mode Decomposition (DMD) and its profound implications. While traditionally embraced by fluid dynamics researchers, DMD’s significance extends far beyond, captivating the interest of data science and data engineering enthusiasts alike. In this article, I will elucidate the broad concepts behind DMD, while also tracing its application within the broader context of data-driven systems and engineering. Throughout this journey, I will draw insights from the book “Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems” by J. Nathan Kutz and others, enriching our understanding with valuable perspectives from leading experts in the field.

Lets begin!!!

History

Dynamic Mode Decomposition (DMD) originated within the fluid dynamics community, initially conceived as a method to deconstruct complex flows into simpler representations grounded in spatiotemporal coherent structures. Pioneered by Schmid (2010), the DMD algorithm was first defined and showcased its efficacy in extracting insights from high-dimensional fluid dynamics data. The burgeoning success of DMD can be attributed to its equation-free, data-driven nature, enabling precise decomposition of complex systems into spatiotemporal coherent structures. These structures hold promise for applications in short-term future-state prediction and control, underscoring the method’s relevance and potential across various disciplines.

At its essence, DMD presents a unique fusion of spatial dimensionality-reduction techniques, such as proper orthogonal decomposition (POD), intertwined with Fourier transforms in time. This integration allows correlated spatial modes to be associated with specific temporal frequencies, potentially accompanied by growth or decay rates. Operationally, DMD, akin to any modal reduction method, relies on gathering snapshots of data from a dynamical system ($x_k$) at various time points ($t_k$, where k = 1, 2, 3, …, m-1 snapshots).

In practice, DMD algorithmically performs a regression of data onto a locally linear dynamical system represented by $x_{k+1} = A x_k$, with the matrix A tailored to minimize the $L_2$ Norm of $\left\lVert x_{k+1} - A x_k \right\rVert _2$ across the m-1 snapshots. The beauty of DMD lies in its straightforward execution, devoid of assumptions about the underlying system’s nature. However, this simplicity comes at the cost of employing Singular Value Decomposition (SVD)/Principal Component Analysis (PCA) algorithms on the snapshot matrix in the background.

PS: The importance of m-1 snapshots will become clearer as we delve into the mathematical intricacies of DMD. For now, let’s treat it as a fundamental aspect of the methodology!

DMD : Applications

Dynamic Mode Decomposition finds its primary applications within three key tasks:

1. Diagnostics
2. Prediction
3. Control

Diagnostics

Since its inception, DMD has been a pivotal diagnostics tool, offering insights into the intricate fluid dynamics of turbulent flow. Much like Proper Orthogonal Decomposition (POD), DMD excels in extracting dominant low-rank spatio-temporal approximations from high-dimensional systems like turbulent flows. This capability enables the physical interpretation of these low-rank dominant features, relating them to spatial structures associated with temporal responses. To illustrate its utility, consider the simple example of tea and honey.

Imagine you’re stirring honey into your tea. At first, the honey flows smoothly and predictably, but as you stir faster, things get chaotic. This chaotic, swirling motion is what we call turbulent flow. This turbulent flow can be broken down into scales:

• Large-scale turbulence: Think of these as the big, swirling motions you see when you stir your tea vigorously. These large-scale motions can be as big as the entire cup, causing noticeable disturbances in the liquid.
• Medium-scale turbulence: Zoom in a bit and focus on smaller whirls within the tea. These medium-scale motions are still pretty significant and can affect how the tea mixes and moves around in the cup.
• Small-scale turbulence: If you zoom in even further, you’ll notice tiny, rapid whirls and eddies forming within the tea. These small-scale motions are like mini tornadoes, constantly churning and mixing the liquid on a very small level.

So, in summary, turbulent flow involves a mixture of large, medium, and small-scale motions, all interacting with each other in a chaotic dance. In nature, turbulent flow can be seen in rivers, oceans, and even the atmosphere. It’s what causes waves to crash on the shore, clouds to form intricate patterns, and wind to swirl unpredictably.

At this juncture, DMD excels in breaking down the complexity of turbulent flow into dominant low-rank spatio-temporal features, thereby aiding in the interpretation (diagnosis) of phenomena occurring during the stirring of tea and honey. Across various fields, DMD primarily serves as a diagnostic tool, enabling the data-driven exploration of fundamental, low-rank structures within complex systems. This diagnostic capability parallels the role of POD analysis in domains such as fluid flows, plasma physics, and atmospheric modeling, among others.

Prediction

A more advanced application of DMD involves utilizing the dominant spatiotemporal structures in the data to construct dynamical or reduced-order models of the observed processes. While challenging, this task is feasible for two specific reasons. Firstly, DMD leverages Singular Value Decomposition (SVD) to extract spatio-temporal low-rank modes from the data, which can then serve as building blocks for constructing a low-rank dynamical model. Secondly, DMD essentially performs regression on the data, aiming to formulate the best-fit (least-square) linear dynamical system that approximates the nonlinear dynamical system generating the data. These characteristics enable DMD to anticipate the future state of the system, even in the absence of measurements.

However, complicating the regression aspect of DMD is the presence of multiscale dynamics in both time and space within the underlying dynamics. Nevertheless, various strategies, such as intelligent data sampling and updating the regression, can mitigate this challenge, enhancing the effectiveness of DMD in generating a useful linear dynamical model. This generative model approach holds promise for predicting future states of dynamical systems and has demonstrated success across numerous application areas.

Control

Direct control of dynamical systems from data sampling represents the pinnacle application of DMD. Suppose, based on the previous applications, we have gained sufficient insight into the nonlinear dynamical system of interest to construct a linear dynamical model for predicting its future state. It’s reasonable to expect that, for a short time in the future, both the nonlinear system and the predicted linear system will agree with each other. The goal is to have this accurate prediction window of sufficient duration to facilitate a control decision capable of influencing the future state of the system by tweaking the system to get intended outcomes. In this scenario, the DMD algorithm enables a wholly data-driven approach to control theory, presenting a compelling mathematical framework for controlling complex dynamical systems where the governing equations are either unknown or computationally challenging to model.

In conclusion, Dynamic Mode Decomposition (DMD) emerges as a versatile and powerful tool with far-reaching implications across various disciplines, from fluid dynamics to control theory. As we’ve explored its foundational concepts and diverse applications in diagnostics, prediction, and control, we’ve only scratched the surface of its potential. In future articles, we will dive deeper into the mathematical intricacies of DMD, unraveling its underlying principles and algorithms. We’ll explore toy examples to illustrate its practical implementation and focus into specific applications, such as diagnostics and prediction.

Stay tuned as we unravel the full spectrum of possibilities that DMD offers, paving the way for groundbreaking advancements in data-driven modeling and control.