Shubham Goswami, PhD

Shubham Goswami, PhD

Postdoctoral Associate at University of Calgary

Python Tools for Analyzing and Visualizing Mesh Motion Simulations

8 minute read

Published:

Postprocessing is a critical step in any simulation workflow, providing insights into the results and enabling effective communication of findings. When it comes to dynamic mesh motion simulations, visualizing the mesh deformation and understanding its effects on flow features can be particularly challenging. In this article, I’ll explore how to use Python for postprocessing such simulations, focusing on extracting, analyzing, and visualizing mesh motion data. With a combination of powerful libraries like Matplotlib, NumPy, and PyVista, we’ll unlock techniques to create meaningful visualizations and derive valuable insights from simulation results.

Dynamic mesh motion simulations provide valuable insights into the interaction between moving boundaries and the surrounding flow. However, the true potential of these simulations is realized only through effective postprocessing, where mesh behavior is analyzed and visualized. In this blog, we’ll focus on extracting, visualizing, and analyzing mesh motion data using Python, showcasing practical techniques to interpret complex deformations and movements. Building on the foundational tutorials from my previous blogs on setting up mesh motion simulations, this article will guide you through postprocessing workflows, enabling you to transform raw data into actionable insights.

II will build upon the tutorial cases introduced in my previous two articles. These include the simulation of flow around a heaving square cylinder (Available here) and flow around a thin flat plate aligned parallel to the flow direction (download here).

Lets Begin!!!

Setting Up the Environment

Before diving into postprocessing, ensure your environment is ready to handle the data efficiently. This involves installing essential Python libraries like:

  • numpy for numerical operations,
  • matplotlib for creating static and animated visualizations,
  • pyvista for handling and visualizing mesh data in 3D, and
  • vtk for working with VTK-formatted files.

For setting up your Python environment, refer to my previous article.

Here’s how you can set up the environment:

pip install numpy matplotlib pyvista vtk

Understanding motion kinematics

Beyond visualization, quantitative analysis can provide deeper insights into the dynamics of mesh motion. For instance, by visualizing the kinematics of mesh motion using Python, you can estimate the period of one pitching or heaving cycle and determine appropriate intervals for data writing. To get started, open a Jupyter notebook and import the necessary modules:

import matplotlib.colors
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import fluidfoam as fl
import scipy as sp
import os
import matplotlib.animation as animation
import pyvista as pv
import imageio
import io
%matplotlib inline

plt.rcParams.update({'font.size' : 18, 'font.family' : 'Times New Roman', "text.usetex": True})
cmap = matplotlib.colors.LinearSegmentedColormap.from_list("", ["cyan", "xkcd:azure", "blue", "xkcd:dark blue", "white", "xkcd:dark red", "red", "orange", "yellow"])

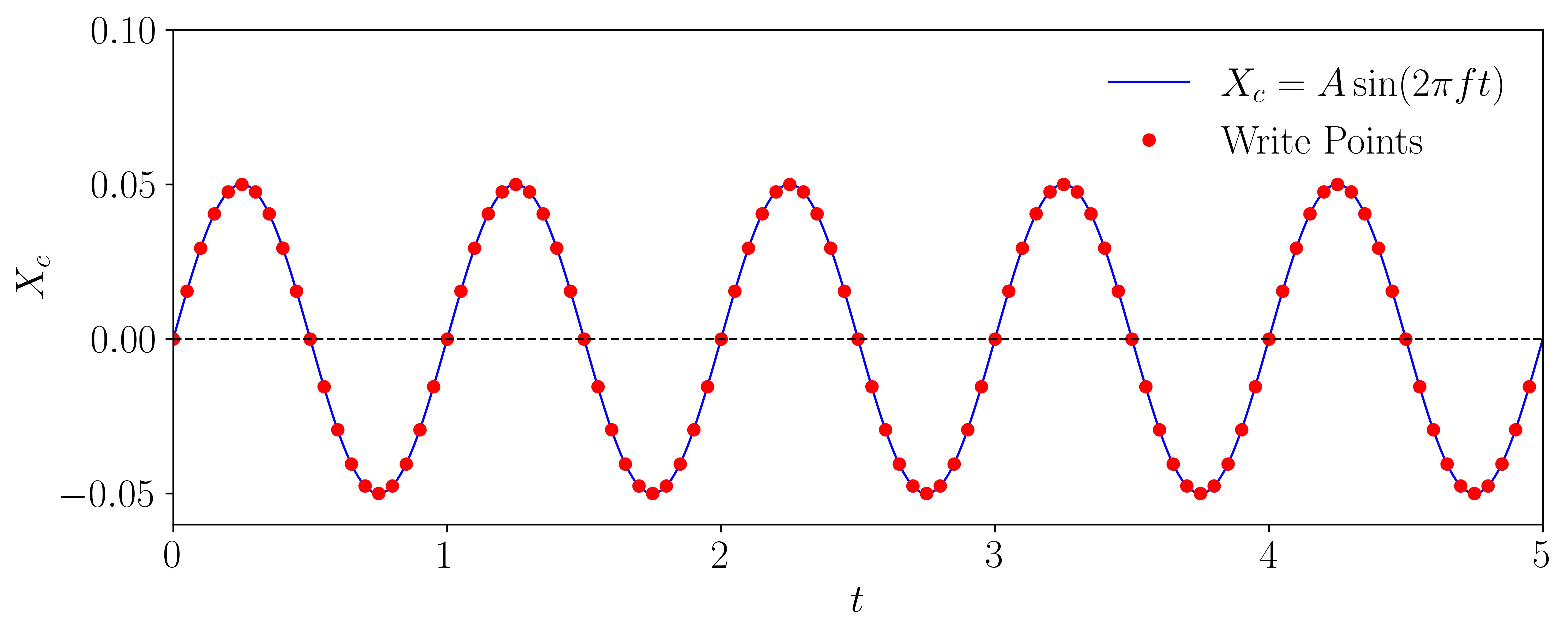
The motion we aim to prescribe follows a sinusoidal wave, mathematically represented as:

\[y(t) = A sin(\omega t)\]

To define the motion, let’s specify the amplitude (A) and the frequency (f) of the sinusoidal wave:

# Motion Xc = A Sin(2*pi*f*t)
A = 0.05
f = 1
omega = 2*np.pi*f
Times = np.arange(0, 5, 0.0004)
Xc = A*np.sin(omega*Times)

Finally, we can plot the motion equation along with markers representing the time intervals at which data will be saved in OpenFOAM:

# Plot 
fig, ax = plt.subplots(figsize = (11, 4))
ax.plot(Times, Xc, label = r'$X_c = A \sin(2\pi f t)$', color = 'blue', linewidth = 1)
MarkEvery = 125
ax.plot(Times, Xc, 'ro', markersize = 5, label = 'Write Points', markevery = MarkEvery)
ax.axhline(y = 0, color = 'black', linestyle = '--', linewidth = 1)
ax.legend(loc='best', frameon = False); # or 'best', 'upper right', etc
ax.set_xlim([0, 5])
ax.set_ylim([-0.06, 0.1])
ax.set_ylabel(r'$X_c$')
ax.set_xlabel(r'$t$')
plt.show()

By visualizing this plot, you can observe the sinusoidal motion profile and identify the specific time intervals for data saving. This approach ensures that the data is captured consistently and aligns with the prescribed motion.

Extracting Mesh Data

The first step in postprocessing is to extract mesh motion data from your simulation. OpenFOAM typically provides this information as displacement fields (pointDisplacement) or velocity fields (motionUx), which can be processed further. For 2D simulations, the foamToVTK utility simplifies this process by converting OpenFOAM case data into VTK format, making it easier to handle in Python. Once converted, you can use Python libraries like pyvista to load and manipulate the data.

However, not all simulations are strictly 2D, and extracting meaningful slices or surfaces from 3D simulations is often necessary. OpenFOAM offers an efficient way to achieve this using the surfaces function object. This tool allows you to extract two-dimensional slices or surfaces from the dataset. To configure it, create a file named <Case>/system/surfaces and set it up as shown below:

surfaces
{
    type            surfaces;
    libs            ("libsampling.so");
    writeControl   	timeStep;
    writeInterval   10;

    surfaceFormat   vtk;
    fields          (p U);

    interpolationScheme cellPoint;

    surfaces
    {
        zNormal
        {
            type        cuttingPlane;
            point       (0 0 0.05);
            normal      (0 0 1);
            interpolate true;
        }
    };
};

You can use this function object during runtime to extract surfaces at specified writeIntervals, or, as in this case, use it as a postprocessing tool after completing your simulation. For instance, if your simulation has reached statistical convergence, you can save surfaces for 50 time directories as follows:

goswami@ME:/mnt/f/Moving_Meshes_OFTest/Org/Org$ ls
0        4.56315  4.96315  5.36315  5.76315  6.16315  6.56315  6.96315  7.36315  7.76315  8.16315
4.24315  4.64315  5.04315  5.44315  5.84315  6.24315  6.64315  7.04315  7.44315  7.84315  constant
4.32315  4.72315  5.12315  5.52315  5.92315  6.32315  6.72315  7.12315  7.52315  7.92315  foam.foam
4.40315  4.80315  5.20315  5.60315  6.00315  6.40315  6.80315  7.20315  7.60315  8.00315  system
4.48315  4.88315  5.28315  5.68315  6.08315  6.48315  6.88315  7.28315  7.68315  8.08315

Once your case is set up, open an OpenFOAM-sourced terminal and execute the following command:

pimpleFoam -postProcess -func surfaces

This command will process the simulation results and write the pressure and velocity data for the specified slice at each time directory. The output will be stored in the <Case>/postProcessing/surfaces/ directory. A sample output might look like this:

goswami@ME:/mnt/f/Moving_Meshes_OFTest/Org/Org/postProcessing/surfaces$ ls
4.24315  4.56315  4.88315  5.20315  5.52315  5.84315  6.16315  6.48315  6.80315  7.12315  7.44315  7.76315  8.08315
4.32315  4.64315  4.96315  5.28315  5.60315  5.92315  6.24315  6.56315  6.88315  7.20315  7.52315  7.84315  8.16315
4.40315  4.72315  5.04315  5.36315  5.68315  6.00315  6.32315  6.64315  6.96315  7.28315  7.60315  7.92315
4.48315  4.80315  5.12315  5.44315  5.76315  6.08315  6.40315  6.72315  7.04315  7.36315  7.68315  8.00315

Each time directory will contain files for the extracted surfaces. For example:

goswami@ME:/mnt/f/Moving_Meshes_OFTest/Org/Org/postProcessing/surfaces$ tree 4.24315/
4.24315/
└── zNormal.vtp

Here, zNormal.vtp is the VTK file containing the pressure and velocity data for the slice at the specified time step.

Now, let’s move to postprocessing in Python. Start by setting up the path variables and constants in your Jupyter notebook. These will help you organize and access the data efficiently in your analysis workflow.

# Path Variables 
Path = 'F:/Moving_Meshes_OFTest/Org/Org/postProcessing/surfaces/'
save_path = 'F:/Moving_Meshes_OFTest/Org/'
save_Blog = 'F:/E_Drive/Blog_Posts/2025_Blogs/Blog9/'
Files = os.listdir(Path)

# Constants
d = 0.1
Ub = 1

To begin, load the data from a single VTK file using the following code:

Data = pv.read(Path + Files[0] + '/zNormal.vtp')
grid = Data.points
x = grid[:,0]
y = grid[:,1]
z = grid[:,2]
rows, columns = np.shape(grid)
print('rows = ', rows, 'columns = ', columns)

To extract and compute the vorticity for all time steps, use PyVista within a loop. This approach enables the creation of a matrix containing the vorticity data:

Data = pv.read(Path + Files[0] + '/zNormal.vtp')
grid = Data.points
x = grid[:,0]
y = grid[:,1]
z = grid[:,2]
rows, columns = np.shape(grid)
print('rows = ', rows, 'columns = ', columns)

### For U
Snaps = len(Files)
data_Vort = np.zeros((rows,Snaps-1))
grid_x = np.zeros((rows,Snaps-1))
grid_y = np.zeros((rows,Snaps-1))
grid_z = np.zeros((rows,Snaps-1))
for i in np.arange(0,Snaps-1):
    data = pv.read(Path + Files[i] + '/zNormal.vtp')
    grid = data.points
    grid_x[:,i:i+1] = np.reshape(grid[:,0], (rows,1), order='F')
    grid_y[:,i:i+1] = np.reshape(grid[:,1], (rows,1), order='F')
    grid_z[:,i:i+1] = np.reshape(grid[:,2], (rows,1), order='F')
    gradData = data.compute_derivative('U', vorticity=True)
    grad_pyvis = gradData.point_data['vorticity']
    data_Vort[:,i:i+1] = np.reshape(grad_pyvis[:,2], (rows,1), order='F')

np.save(save_path + 'VortZ.npy', data_Vort)
np.save(save_path + 'grid_x.npy', grid_x)
np.save(save_path + 'grid_y.npy', grid_y)
np.save(save_path + 'grid_z.npy', grid_z)

After extracting the data, visualize the vorticity field with a contour plot:

Contour = 0
A = 0.05/0.1
Omega = 2*np.pi

fig, ax = plt.subplots(figsize=(11, 4))
p = ax.tricontourf(grid_x[:,Contour]/0.1, grid_y[:, Contour]/0.1, data_Vort[:,Contour]*(d/Ub), 
                   levels = 1001, vmin=-1.8, vmax=1.8, cmap = cmap)
patches = []
patches.append(plt.Rectangle((-0.5, (A*np.sin(Omega*float(Files[Contour])))-0.5), 1, 1, 
                             ec='k', color='white', zorder=2))
ax.add_patch(patches[0])
ax.xaxis.set_tick_params(direction='in', which='both')
ax.yaxis.set_tick_params(direction='in', which='both')
ax.xaxis.set_ticks_position('both')
ax.yaxis.set_ticks_position('both')
ax.set_xlim(-1, 20)
ax.set_ylim(-5, 5)
ax.set_aspect('equal')
ax.set_xlabel(r'$x/d$')
ax.set_ylabel(r'$y/d$')
fig.set_tight_layout(True)
plt.savefig(save_Blog + 'SqCylPlot.jpeg', dpi = 600, bbox_inches = 'tight')
plt.show()

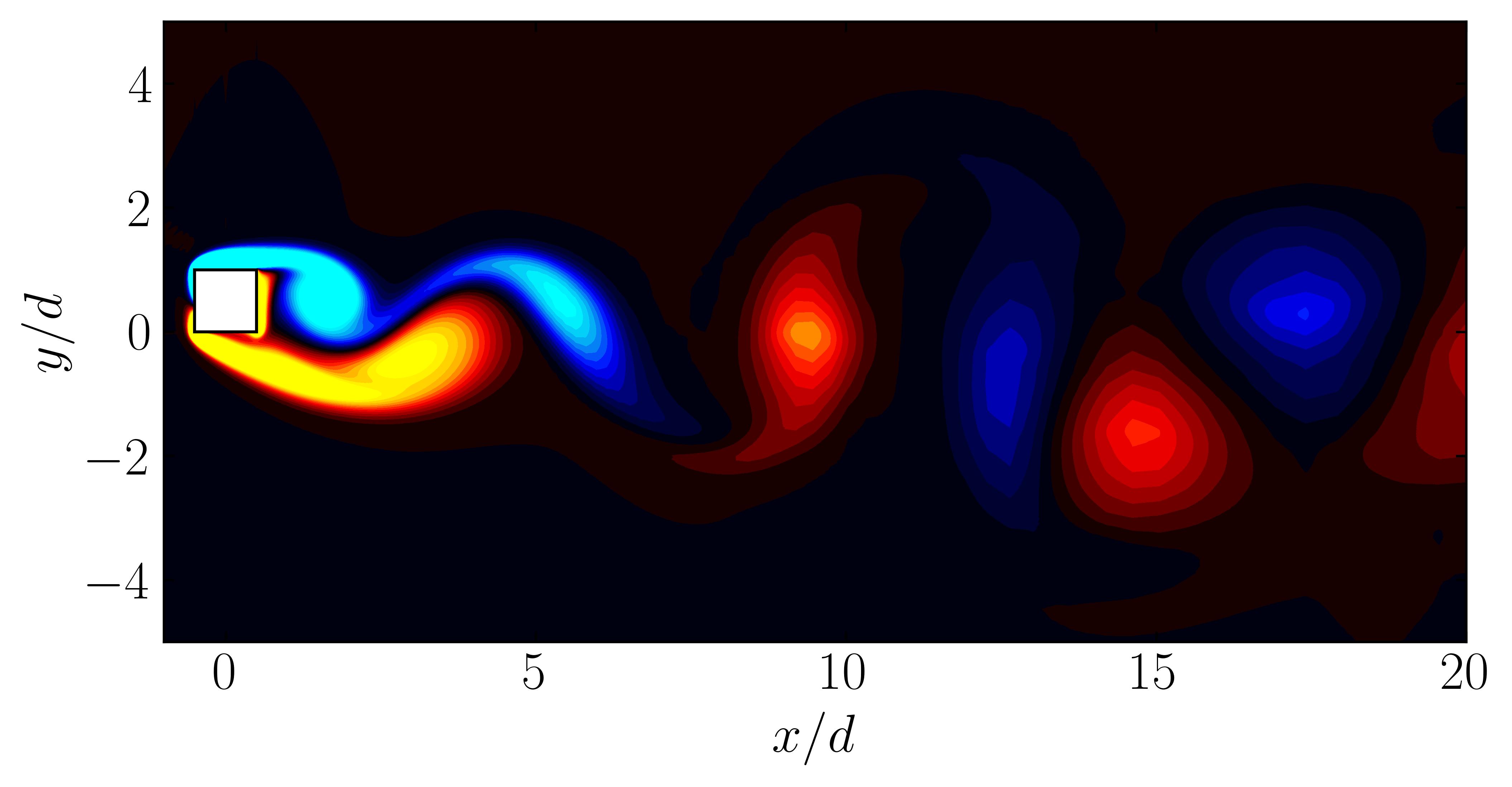
Since we are working with moving meshes, it’s crucial to account for the prescribed motion. For a sinusoidal motion, the position of the square cylinder at any time instant can be calculated using:

\[X_c = A sin(\omega T)\]

This enables precise positioning of the square cylinder patch in the plot. The same process can be followed for pure pitching and pure heaving simulations.

You May Also Enjoy

Setting Up Overset Mesh Cases in OpenFOAM Made Easy

16 minute read

Published:

Overset mesh, also known as chimera or overlapping grid, is a powerful technique in CFD for handling complex geometries and moving bodies without remeshing. This capability in OpenFOAM simplifies simulations involving relative motion between components, such as propellers or rotor-stator interactions. In this article, I will explore the step-by-step process of setting up an overset mesh case in OpenFOAM, focusing on essential parameters, best practices, and potential pitfalls.

An Introduction to Overset Mesh in OpenFOAM

5 minute read

Published:

Dynamic mesh motion is a critical feature in computational fluid dynamics (CFD) for simulating problems with moving boundaries or complex geometries. Among the various techniques available in OpenFOAM, the Overset mesh approach has gained popularity due to its flexibility in handling relative motion between different mesh regions. This method allows engineers and researchers to solve problems like rotor-stator interactions, aerodynamic analysis of moving vehicles, and more with enhanced accuracy and efficiency. In this blog, I’ll explore the fundamentals of Overset meshes in OpenFOAM.

Simulating Pure Pitching and Heaving Motions in OpenFOAM

9 minute read

Published:

Dynamic mesh techniques in Computational Fluid Dynamics (CFD) are pivotal for capturing fluid-structure interactions and other phenomena involving motion. In OpenFOAM, the prescribed motion method allows users to simulate complex scenarios using deformable meshes while maintaining computational efficiency. This article further explores the prescribed mesh motion technique, with a specific focus on simulating pure pitching and pure heaving motions. By the end of this guide, you’ll gain insights into implementing these motions in OpenFOAM and understanding their impact on flow dynamics.

Dynamic Meshes in OpenFOAM: A Deep Dive into Prescribed Mesh Motion

12 minute read

Published:

Simulating real-world fluid dynamics problems often requires the ability to handle dynamic changes in the computational domain. OpenFOAM’s dynamic mesh capabilities provide the necessary tools for this purpose. This blog explores the fascinating concept of dynamic mesh motion in OpenFOAM, specifically the mesh deformation method using prescribed motion technique. I will showcase the case setup and provide a general overview of simulating mesh motion in OpenFOAM.